¹Department of Psychology, State University of Humanities and Social Studies (SUHSS). Zelenaya str., 30, Kolomna-140410, Russia

²Avalon Business Systems, Inc. 18-11 Radburn Road, Fair Lawn, NJ 07410, USA

*Corresponding author: Eugen Tarnow, Avalon Business Systems, Inc. 18-11 Radburn Road, Fair Lawn, NJ 07410, USA, Phone: +16462290787, E-mail: [email protected]

Received: June 19, 2025

Published: July 21, 2025

Citation: Ershova R, et al. (2025). Working Memory Capacities of Teaching College Students Differ by Academic Field: High School Sports Teachers on Top. Neuro Research. 7(1):24.

Copyright: Ershova R, et al. © (2025).

ABSTRACT

The working memory capacity (WMC) of 480 Russian teacher college students as well as 19 law students was measured using the Tarnow Unchunkable Test (TUT), which measures the free recall of unrelated double-digit integers. The academic fields of the students were found to account for about 5% (9%) of the variance in the average WMC for the 3-item (4-item) test. WMC increased in the order vocational, K-5, chemistry, mathematics, philology, psychology, history, law, computer science, physics and sports. The future teaching level (kindergarten, grades 1-5, grades 6-12 and vocational) accounted for 2.2% (5.5%) of the variance in the 3-item (4-item) test. We apply the TUT to the university as a whole and find that the university tends to encourage applications from high WMC fields.

Keywords: Working Memory Capacity, Working Memory Test

INTRODUCTION

If the reader attempts to remember four unrelated double digit integers (the Tarnow Unchunkable Test, [1]), it is very probable that one of the integers vanishes, no matter how hard the reader tries. This almost magical process shows that most of us have three memory pointers [2] for similar items. If we try to force in another item into our “working memory”, interference occurs and removes one of the other items - somehow.

We distinguish between two types of working memory capacity: working memory capacity measured in tasks that also include a variety of operations such as arithmetic problem solving or sentence content analysis which we call working memory operational capacity (WMOC) as opposed to working memory capacity measured without such operations which we call working memory capacity (WMC).

WMOC is thought to be strongly correlated with general fluid intelligence and novel reasoning, perhaps via attentional control [3]. It is found that WMOC can be lowered by math anxiety [4,5]; stereotype threat [6] and sometimes increased by physical exercise [7]. The relationship of WMC (as opposed to WMOC) to intelligence is, as far as the authors know, unknown. While there has been work correlating forward digit span to intelligence (see, for example, [8]), the forward digit span is not a pure WMC measure since the digits can be chunked together.

WMC is measured differently by different researchers, some use simple free recall as a measure. Free recall consists of two stages, only the first corresponds to working memory, the second is a reactivation process presumably using associations [9]. In this contribution we use the TUT which attempts to eliminate the possibility of associations and the activation of the second stage.

In this contribution we investigate how WMC varies with academic field for students in a teaching college preparing to teach high school physics, mathematics, computer science, vocational, history, sports, psychology and grade school and kindergarten.

Early and mid 1900s saw a lot of interest in aptitude testing, for example for military personnel assignments. US government sponsored test batteries such as the General Aptitude Test Battery, which includes a numerical component, became important and were also used for job placement within the government.

There does not appear to be any published work on how WMOC varies with academic field. There is work on IQ of eminent physicists, biologists, psychologists and anthropologists [10] with a corresponding ranking of the fields: theoretical physics, anthropology, psychology, biology and experimental physics. There are also jokes about Einstein, IQ and field areas usually putting physics on top.

Aptitude testing waned in the 1960s due to concerns about civil rights and workplace discrimination. Current occupational psychology focus on cognition within occupation related to documenting effects of exposures, accident avoidance and rehabilitation and not on cognitive testing of normal individuals. Educational placement is often limited to intra-field placements rather than inter-field placements and often focused on populations that are cognitively non-normal. Career choices are studied by survey, not by cognitive testing.

Our investigation may be important for understanding the structure of academic fields, the structure of WM, for designing new empirical studies to advance theory and research in this area, as well as measuring the effectiveness of the methodological tools needed to test WM.

METHOD

We present data from a study of university students aged 17 to 24.

The Tarnow Unchunkable Test (TUT) used in this study separates out the working memory (WM) component of free recall by using particular double-digit combinations which lack intra-item relationships [1]. It does not contain any explicit WM operations. The TUT was given via the internet using client-based JAVAScript to eliminate any network delays. The instructions and the memory items were displayed in the middle of the screen. Items were displayed for two seconds without pause. The trials consisted of 3 or 4 items after which the subject was asked to enter each number remembered separately, press the keyboard enter button between each entry and repeat until all the numbers remembered had been entered. Pressing the enter button without any number was considered a "no entry". The next trial started immediately after the last entry or after a "no entry". There was no time limit for number entry. Each subject was given six three item trials and three four item trials in which the items are particular double-digit integers.

Sample

480 Russian undergraduate teaching college students of the State University of Humanities and Social Studies 67% females and 33%) males, mean age was 18.8 years) and 19 law students participated in the study for extra credit. Each participant was tested individually in a quiet room. An experimenter was present throughout each session.

One record was discarded – the student had only responded once out of a possible thirty times.

We had no hypothesis about this research so we did not estimate the sample size needed in advance. The statistics reported includes the effect of the sample size. The sample size is relatively large.

RESULTS

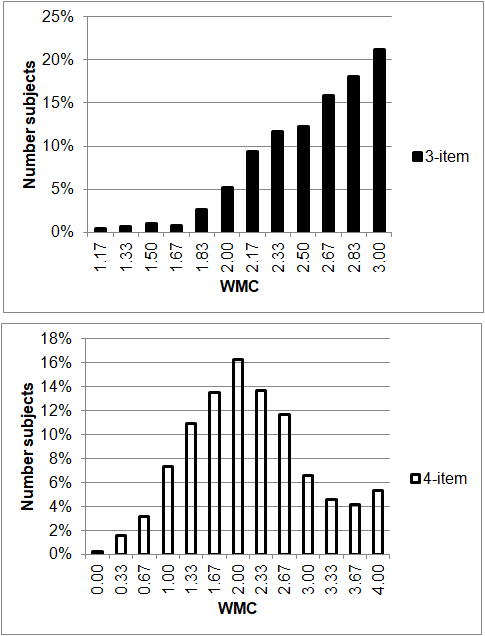
Using a one-way ANOVA we find that different fields account for 5-9% of the variance (F=1.9 p=.011, η²=0.057 for the 3-item test and F=3.2 and p<0.001, η²=0.093 for the 4-item test). There is a 0.73 correlation between the 3-item and 4-item recalls averaged over field. The histograms of the 3-item and 4-item tests are shown below. For both of them there is a ceiling effect and for the 3-item test the ceiling effect questions whether we can use the normal distribution requirements of the ANOVA (to which the ANOVA is relatively insensitive). Thus we also performed a Kruskal-Wallis test (adjusted for ties). The null hypothesis for the 3-item test was again rejected (p=0.008; for completeness, p<0.001 for the 4-item test).

Figure 1. Histograms of 3- and 4-item recalls.

Cronbach’s alpha is 0.475 for the 3-item test and 0.494 for the 4-item test. For both combined it is 0.587.

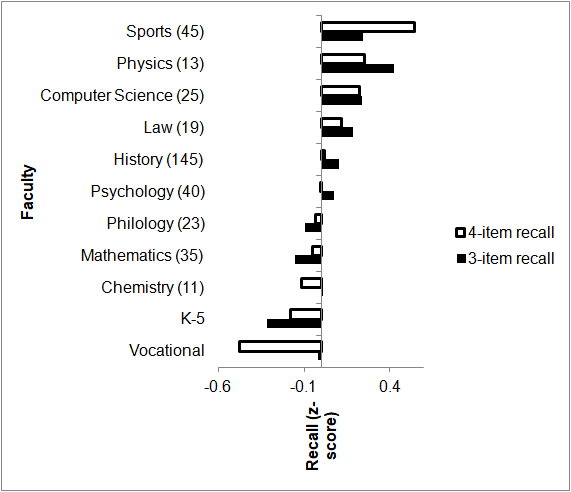
The corresponding z-scores (calculated using the individual distribution standard deviation) for the fields are shown in Figure 2, ranging from vocational to sports.

Figure 2. Average recall z scores for students in different fields. The number of subjects in each field is indicated in the parentheses. The fields are ordered based on the 4-item recall. z is based on the individual standard deviation.

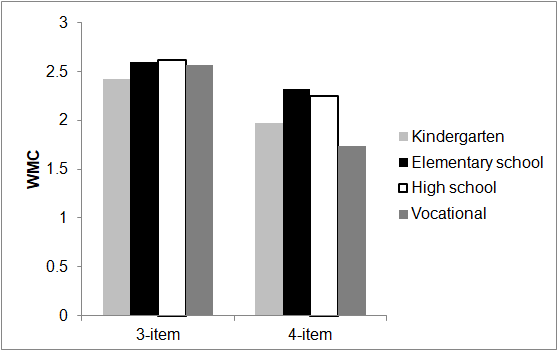
We also performed an ANOVA of teaching level (kindergarten, grades 1-5, grades 6-12 and vocational) and found that teaching level accounted for 2.2% (5.5%) of the variance in the 3-item (4-item test) with F=2.84, p<0.015, η²= =0.022 (F=7.22, p<0.001, η²=0.055). The 3-item and 4-item TUT results by teaching level are displayed in Figure 3.

Figure 3. 3-item and 4-item TUT results by teaching level.

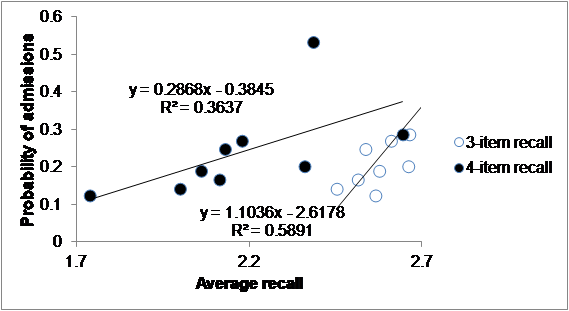
We can change the level of our perspective and consider how the field admissions of the university correlate with field recall averages (Table 1). The number of admitted students in each field is only weakly correlated with WMC and the sign of the correlations are different or the 3-item and 4-item tests. Thus overall the university admits students irrespective of WMC. However, the field acceptance rates are strongly correlated with field WMC (see also Figure 4) - it is easier to enter as a student in a high WMC field than in a low WMC field. This probably means that though the university would prefer more students in high WMC fields, it cannot get enough applicants in these fields. This would also explain why the GPA average field admissions test score correlates negatively with field WMC – the high WMC fields allow for lower GPA admission test scores. Correlation between the field rate of admission with GPA admission test score is -0.28.

Table 1. Correlations by field averages.

	3-item recall (field average)	4-item recall (field average)
Total number of students accepted by field	-.23	.21
Field acceptance rate	0.76	0.54
Field average GPA admissions score	-0.47	-0.08

Figure 4. Probability of admission as a function of the average recall for the different fields.

DISCUSSION

We found that academic field accounts for 5-9% of the variance in WMC. The field that scored the highest was sports and the field that scored the lowest was vocational. The level of future instruction accounted for 2-5% of the variance with 6^th-12^th grade level being the highest and vocational the lowest.

We do not know why sports teaching students score the highest and vocational teaching students the lowest on our WMC test. Previous work shows that exercise increases working memory capacity [11] and it could also be that sports tend to associate more meaning with double integer numbers than the other fields (but then should not mathematics be the highest performing?), that a high WMC is more important in sports than in vocational jobs (in team sports it may be important to keep in mind the position of several players), etc.

The TUT opens up a new, relatively inexpensive way to investigate human endeavors. It seems that the university increases the probability of admission for the high WMC fields and decreases it for low WMC fields.

CONCLUSION

The working memory capacity (WMC) of 480 Russian teacher college students as well as 19 law students was measured using the Tarnow Unchunkable Test (TUT), which measures the free recall of unrelated double-digit integers. The academic fields of the students were found to account for about 5% (9%) of the variance in the average WMC for the 3-item (4-item) test. WMC increased in the order vocational, K-5, chemistry, mathematics, philology, psychology, history, law, computer science, physics and sports. The future teaching level (kindergarten, grades 1-5, grades 6-12 and vocational) accounted for 2.2% (5.5%) of the variance in the 3-item (4-item) test.

We apply the TUT to the university as a whole and find that the university tends to encourage applications from high WMC fields.

The question remains as to why there is a WMC difference for the various academic fields. Is not working memory a fundamental property of the brain, and thus should be the same for all fields?

If WMC differences are important for the different fields, what does that say about AI [11,12]? Since AI is limitless in its working memory, maybe it would be very good at sports?

ACKNOWLEDGEMENTS

None.

CONFLICT OF INTEREST

The authors declare that there is no conflict of interest.

REFERENCES

1. Tarnow E. (2013). U.S. Patent Application No. 14/066,195.
2. Ershova RV, Tarnow E. (2016). Working Memory Capacity Test Reveals Subjects Difficulties Managing Limited Capacity. Bulletin of Peoples' Friendship University of Russia. Series: Psychology and Pedagogy. (3).
3. Kane MJ, Hambrick DZ, Conway ARA. (2005). Working memory capacity and fluid intelligence are strongly related constructs: comment on Ackerman, Beier, and Boyle (2005). Psychol Bull. 131(1):66-71.
4. Ashcraft MH, Kirk EP. (2001). The relationships among working memory, math anxiety, and performance. Journal of experimental psychology: General. 130(2):224-237.
5. Miller H, Bichsel J. (2004). Anxiety, working memory, gender, and math performance. Personality and Individual Differences. 37(3):591-606.
6. Schmader T, Johns M. (2003). Converging evidence that stereotype threat reduces working memory capacity. J Pers Soc Psychol. 85(3):440-452.
7. Sibley BA, Beilock SL. (2007). Exercise and working memory: an individual differences investigation. J Sport Exerc Psychol. 29(6):783-791.
8. Jensen AR, Figueroa RA. (1975). Forward and backward digit span interaction with race and IQ: predictions from Jensen's theory. J Educ Psychol. 67(6):882-893.
9. Tarnow E. (2015). First direct evidence of two stages in free recall. RUDN Journal of Psychology and Pedagogics. 2015(4):15-26.
10. Roe A. (1953). A psychological study of eminent psychologists and anthropologists, and a comparison with biological and physical scientists. Psychological Monographs: General and Applied. 67(2):1-55.
11. Lambourne K. (2006). The relationship between working memory capacity and physical activity rates in young adults. J Sports Sci Med. 5(1):149-153.
12. KJ McNamara, RP Marpu. (2025). Demystifying AI Agents: The Final Generation of Intelligence. arXiv preprint: https://www.arxiv.org/abs/2505.09932
13. KJ McNamara, RP Marpu. (2025). Exponential Shift: Humans Adapt to AI Economies. arXiv preprint: https://arxiv.org/abs/2504.08855